ナヴィエ・ストークス方程式の直接数値計算と原始惑星系円盤乱流中のダスト成長の研究

図 1  乱流の直接数値計算（格子点数：$2048^3$, レイノルズ数：16100）によって得られた慣性粒子（左から St = 0.01, 0.06, 0.12, 0.24）のクラスタリング。St はストークス数（粒子の制動時間をエネルギー保有渦のタイムスケールで規格化したもの）。

ダスト粒子の合体成長は，微惑星形成にとって不可欠なプロセスであるが，１）ダストが合体成長する前に中心星に落ちる（中心星落下問題），２）衝突の際に付着せずに破壊を起こしてしまう（衝突破壊問題）という困難があり，これらはまだ解決されていない。特に，地球のような岩石惑星の元となるシリケイト・ダストは，限界付着速度が低いため衝突破壊問題が深刻である。原始惑星系円盤内でのダスト粒子の衝突速度は，円盤内の乱流によって決まっているため，乱流によるダスト粒子のクラスタリング（図１）を正しく取り扱う必要がある。そのためには，ナヴィエ・ストークス方程式の直接数値計算が必要となる。宇宙分野では，これまで数値流体計算で粘性項を含まないオイラー方程式が主として用いられてきたが，我々はナヴィエ・ストークス方程式の直接数値計算（DNS）を実現し，乱流中のダスト粒子の運動を正確に追跡した（Ishihara et al. 2018）。DNSの結果，２粒子間の相対速度は，これまで使われてきたOrmel & Cuzzi （2007）の結果の1/2以下に下がることが分かった。これは，乱流によるダスト粒子のクラスタリング効果により，速度分布がマックスウェル分布にならないことに起因する。これにより，これまでダスト成長が起こらないとされてきた強い乱流状態にあっても，合体成長が可能であることが明らかとなった（図２）。この結果は，ダスト粒子の合体成長でセンチメートル・サイズの石ころ（pebble）が形成されることを意味し，ストリーミング不安定による微惑星形成を可能にする。

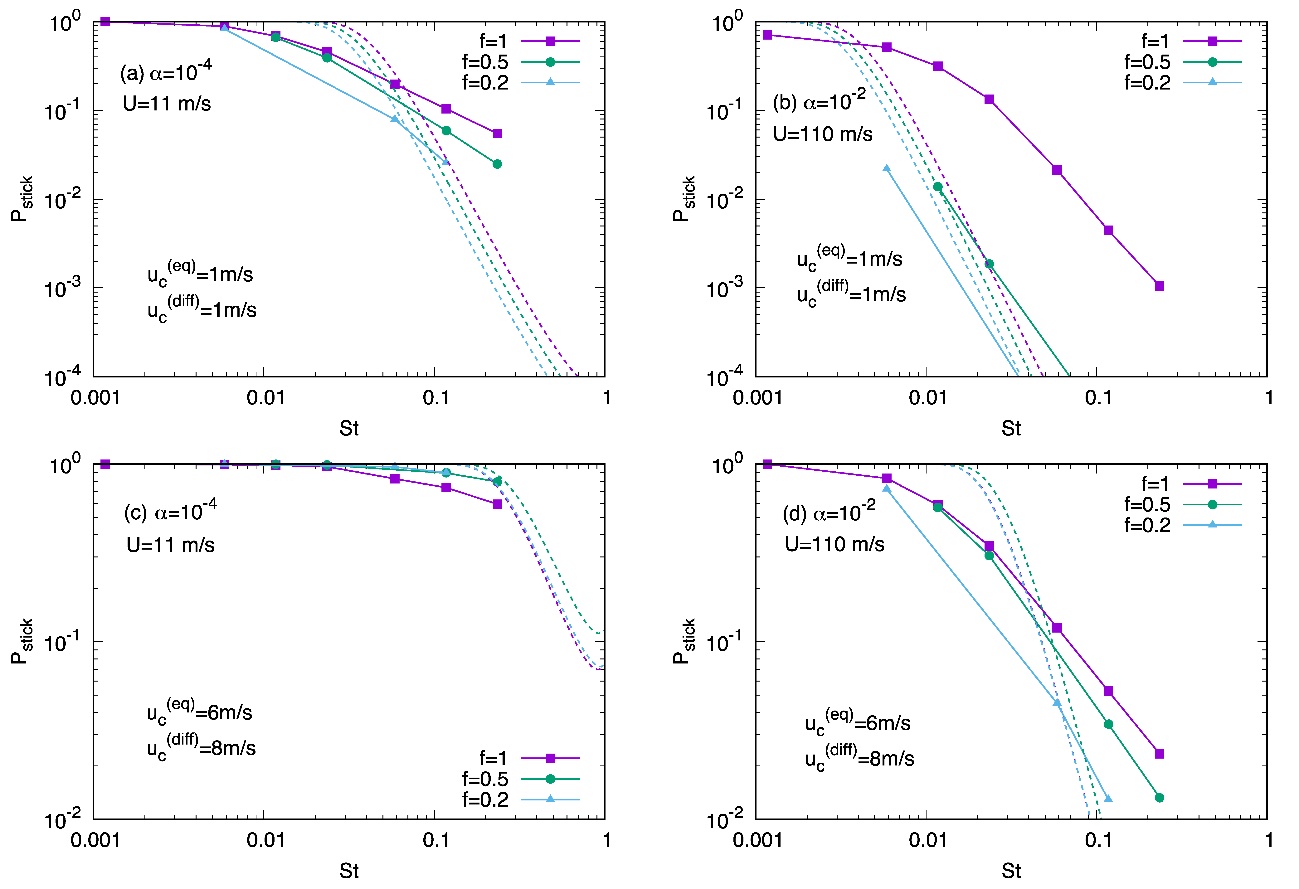
図 2  粒子の大きさ（ストークス数）に対する付着確率。実線はDNSの結果，破線はこれまでの結果（Ormel & Cuzzi 2007）。$f$ は衝突する2粒子のサイズ比（$f = $St$_2 / $St$_1$）。(a), (b) はコンパクトなダストの結果で，(a) は弱い乱流（$\alpha = 10^{-4}$），(b)は強い乱流（$\alpha = 10^{-2}$）の場合。 (c), (d) は空隙のあるダストの結果で，(c) は弱い乱流（$\alpha = 10^{-4}$），(d) は強い乱流（$\alpha = 10^{-2}$）の場合。(b) のコンパクトダストで強い乱流の場合でも高い付着確率が実現する。

参考文献・リンク

1. T. Ishihara, N. Kobayashi, K. Enohata, M. Umemura, & K. Shiraishi, The Astrophysical Journal, vol. 854, 81 (2018)