Navier–Stokes Simulations of Dust Coagulation in a Turbulent Protoplanetary Disk

Fig. 1  Turbulent clustering of dust particles in direct numerical simulations (DNSs) using $2048^3$ grid cells (Reynolds number Re = 16100). From left to right, the Stokes numbers are St = 0.01, 0.06, 0.12, 0.24, respectively.

The coagulation of dust particles is a key process in planetesimal formation. However, the radial drift and bouncing barriers are not completely resolved, especially for silicate dust. Since the collision velocities of dust particles are regulated by turbulence in a protoplanetary disk, turbulent clustering should be properly treated. To that end, direct numerical simulations (DNSs) of the Navier–Stokes equations are requisite. We perform DNSs with up to Reynolds number Re = 16,100, which allow us to track the motion of particles with Stokes numbers of $0.01 \le$ St $\le 0.2$ in the inertial range (Ishihara et al. 2018). Through the DNSs, we confirm that the rms relative velocity of particle pairs is smaller by more than a factor of two, compared to that by Ormel & Cuzzi (2007). The distributions of the radial relative velocities are highly non-Gaussian. We find that even in the strong-turbulence case with $\alpha$-viscosity of $10^{−2}$, the sticking rates are as high as ∼50% and the bouncing probabilities are as low as ∼10% (Fig. 2). Thus, turbulent clustering plays a significant role in the growth of centimeter-sized compact aggregates (pebbles) and also enhances the solid abundance, which may lead to the streaming instability in a disk.

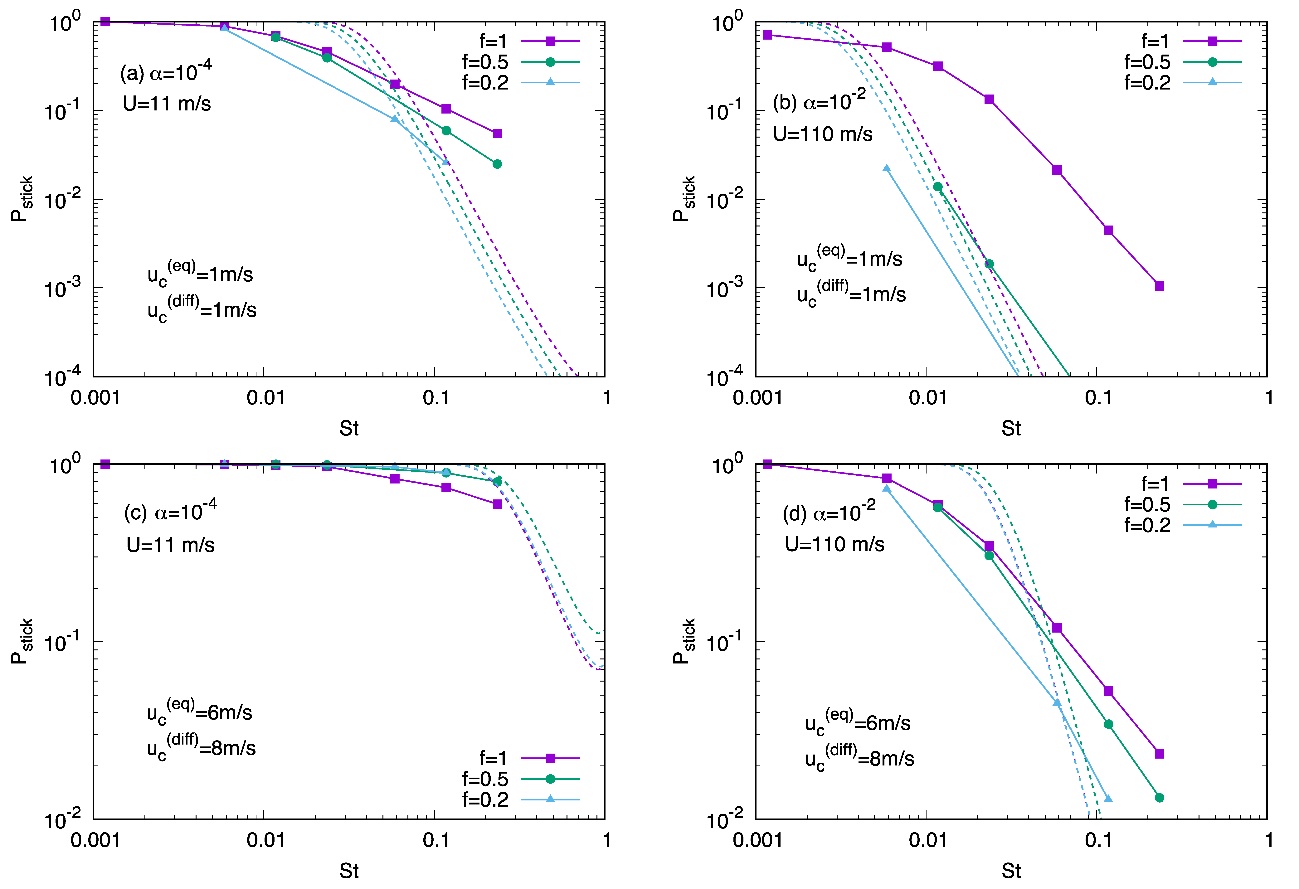
Fig. 2  Sticking rates of colliding particles as functions of St and $f = $St$_2 / $St$_1$, for the case of compact dust (a and b), where the viscous parameter in (a) is $\alpha = 10^{-4}$ and in (b) is $\alpha = 10^{-2}$. The panels (c) and (d) are for the case of fluffy dust, with the same two viscous parameters, respectively. $u_c$ is the critical collision velocity. Colored solid curves represent the DNS results. Colored dotted curves are the theoretical prediction assuming a Gaussian (Maxwell) distribution whose variance is given by Ormel & Cuzzi (2007).

References

1. T. Ishihara, N. Kobayashi, K. Enohata, M. Umemura, & K. Shiraishi, The Astrophysical Journal, vol. 854, 81 (2018)